圆锥曲线中的热点问题

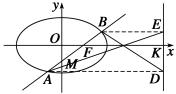
圆锥曲线中的热点问题

考点一　圆锥曲线的弦长及中点问题

例1　已知椭圆G：＋＝1(a>b>0)的离心率为，右焦点(2，0)，斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P(－3,2)．

(1)求椭圆G的方程；

(2)求△PAB的面积．

解　(1)由已知得c＝2，＝.

解得a＝2，又b2＝a2－c2＝4.

所以椭圆G的方程为＋＝1.

(2)设直线l的方程为y＝x＋m.

由

得4x2＋6mx＋3m2－12＝0.①

设A，B的坐标分别为(x1，y1)，(x2，y2)(x1<x2)，AB中点为E(x0，y0)，

则x0＝＝－，y0＝x0＋m＝；

因为AB是等腰△PAB的底边，

所以PE⊥AB.

所以PE的斜率k＝＝－1.

解得m＝2.

此时方程①为4x2＋12x＝0.

解得x1＝－3，x2＝0.

所以y1＝－1，y2＝2.

所以|AB|＝3.

此时，点P(－3,2)到直线AB：

x－y＋2＝0的距离d＝＝，

所以△PAB的面积S＝|AB|·d＝.

解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．

练习1：椭圆＋y2＝1的弦被点平分，则这条弦所在的直线方程是____________．

解:设弦的两个端点为A(x1，y1)，B(x2，y2)，

则x1＋x2＝1，y1＋y2＝1.

∵A，B在椭圆上，∴＋y＝1，＋y＝1.

＋(y1＋y2)(y1－y2)＝0，

即＝－＝－，

即直线AB的斜率为－.

∴直线AB的方程为y－＝－，

即2x＋4y－3＝0.

考点二　圆锥曲线中的定值、定点问题

例2　已知椭圆C：＋＝1经过点(0，)，离心率为，直线l经过椭圆C的右焦点F交椭圆于A、B两点，点A、F、B在直线x＝4上的射影依次为D、K、E.

(1)求椭圆C的方程；

(2)若直线l交y轴于点M，且＝λ，＝μ，当直线l的倾斜角变化时，探求λ＋μ的值是否为定值？若是，求出λ＋μ的值；否则，说明理由；

(3)连接AE、BD，试探索当直线l的倾斜角变化时，直线AE与BD是否相交于定点？若是，请求出定点的坐标，并给予证明；否则，说明理由．

(1)待定系数法；(2)用直线的斜率为参数建立直线方程，代入椭圆方程消y后可得点A，B的横坐标的关系式，然后根据向量关系式＝λ，＝μ把λ，μ用点A，B的横坐标表示出来，只要证明λ＋μ的值与直线的斜率k无关即证明了其为定值，否则就不是定值；(3)先根据直线l的斜率不存在时的特殊情况，看两条直线AE，BD的交点坐标，如果直线AE，BD相交于定点的话，这个特殊位置时的交点就是这个定点，这样只要证明直线AE，BD都经过这个定点即证明了两直线相交于定点，否则两直线就不相交于定点．

解　(1)依题意得b＝，e＝＝，a2＝b2＋c2，

∴a＝2，c＝1，∴椭圆C的方程为＋＝1.

(2)因直线l与y轴相交，故斜率存在，设直线l方程为

y＝k(x－1)，求得l与y轴交于M(0，－k)，

又F坐标为(1,0)，设l交椭圆于A(x1，y1)，B(x2，y2)，

由消去y得(3＋4k2)x2－8k2x＋4k2－12＝0，

∴x1＋x2＝，x1x2＝，

又由＝λ，∴(x1，y1＋k)＝λ(1－x1，－y1)，

∴λ＝，同理μ＝，

∴λ＋μ＝＋＝

＝＝－.

所以当直线l的倾斜角变化时，直线λ＋μ的值为定值－.

(3)当直线l斜率不存在时，直线l⊥x轴，则ABED为矩形，由对称性知，AE与BD相交于FK的中点N，

猜想，当直线l的倾斜角变化时，AE与BD相交于定点N，

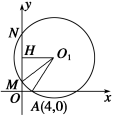
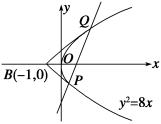
证明：由(2)知A(x1，y1)，B(x2，y2)，

∴D(4，y1)，E(4，y2)，当直线l的倾斜角变化时，首先证直线AE过定点，

∵lAE：y－y2＝(x－4)，

当x＝时，y＝y2＋·

＝

＝

＝

＝＝0.

∴点N在直线lAE上．

同理可证，点N也在直线lBD上．

∴当直线l的倾斜角变化时，直线AE与BD相交于定点.

(1)定值问题就是在运动变化中寻找不变量的问题，基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关．在这类试题中选择消元的方向是非常关键的．

(2)由直线方程确定定点，若得到了直线方程的点斜式：y－y0＝k(x－x0)，则直线必过定点(x0，y0)；若得到了直线方程的斜截式：y＝kx＋m，则直线必过定点(0，m)．

(2013·陕西)已知动圆过定点A(4,0)，且在y轴上截得弦MN的长为8.

(1)求动圆圆心的轨迹C的方程；

(2)已知点B(－1,0)，设不垂直于x轴的直线l与轨迹C交于不同的两点P，Q，若x轴是∠PBQ的角平分线，证明：直线l过定点．

(1)解　如图，设动圆圆心为O1(x，y)，由题意，得|O1A|＝|O1M|，

当O1不在y轴上时，过O1作O1H⊥MN交MN于H，则H是MN的中点，∴|O1M|＝，又|O1A|＝，

∴＝，化简得y2＝8x(x≠0)．

又当O1在y轴上时，O1与O重合，点O1的坐标为(0,0)也满足方程y2＝8x，∴动圆圆心的轨迹C的方程为y2＝8x.

(2)证明　由题意，设直线l的方程为y＝kx＋b(k≠0)，

P(x1，y1)，Q(x2，y2)，

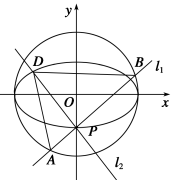
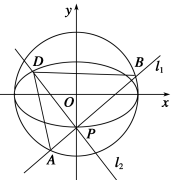
将y＝kx＋b代入y2＝8x中，

得k2x2＋(2bk－8)x＋b2＝0.

其中Δ＝－32kb＋64>0.

由根与系数的关系得，x1＋x2＝， ① x1x2＝， ②

因为x轴是∠PBQ的角平分线，所以＝－，

即y1(x2＋1)＋y2(x1＋1)＝0，

(kx1＋b)(x2＋1)＋(kx2＋b)(x1＋1)＝0，

2kx1x2＋(b＋k)(x1＋x2)＋2b＝0 ③

将①，②代入③得2kb2＋(k＋b)(8－2bk)＋2k2b＝0，

∴k＝－b，此时Δ>0，

∴直线l的方程为y＝k(x－1)，即直线l过定点(1,0)．

考点三　圆锥曲线中的最值范围问题

例3　(2013·浙江)如图，点P(0，－1)是椭圆

C1：＋＝1(a>b>0)的一个顶点，C1的长轴

是圆C2：x2＋y2＝4的直径．l1，l2是过点

P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.

(1)求椭圆C1的方程；

(2)求△ABD面积取最大值时直线l1的方程．

解　(1)由题意得

所以椭圆C1的方程为＋y2＝1.

(2)设A(x1，y1)，B(x2，y2)，D(x0，y0)．

由题意知直线l1的斜率存在，不妨设其为k，

则直线l1的方程为y＝kx－1.

又圆C2：x2＋y2＝4，

故点O到直线l1的距离d＝，

所以|AB|＝2＝2.

又l2⊥l1，故直线l2的方程为x＋ky＋k＝0.

由

消去y，整理得(4＋k2)x2＋8kx＝0，故x0＝－.

所以|PD|＝.

设△ABD的面积为S，则S＝·|AB|·|PD|＝，

所以S＝≤＝，

当且仅当k＝±时取等号．

所以所求直线l1的方程为y＝±x－1.

求最值及参数范围的方法有两种：①根据题目给出的已知条件列出一个关于参数的函数关系式，将其代入由题目列出的不等式(即为消元)，然后求解不等式；②由题目条件和结论建立目标函数，进而转化为求函数的值域．

已知椭圆C1与抛物线C2的焦点均在x轴上且C1的中心和C2的顶点均为坐标原点O，从每条曲线上的各取两个点，其坐标如下表所示：

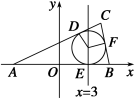
(1)求C1，C2的标准方程；

(2)过点A(m,0)作倾斜角为的直线l交椭圆C1于C，D两点，且椭圆C1的左焦点F在以线段CD为直径的圆的外部，求m的取值范围．

解　(1)先判断出(－，0)在椭圆上，

进而断定点(1，－3)和(4，－6)在抛物线上，故(，1)在椭圆上，

所以椭圆C1的方程为＋＝1，抛物线C2的方程为y2＝9x.

(2)设C(x1，y1)，D(x2，y2)，直线l的方程为y＝(x－m)，

由消去y整理得2x2－2mx＋m2－6＝0，

由Δ>0得Δ＝4m2－8(m2－6)>0， 即－2<m<2， ①

而x1x2＝，x1＋x2＝m，

故y1y2＝(x1－m)·(x2－m)

＝[x1x2－m(x1＋x2)＋m2]＝.

欲使左焦点F在以线段CD为直径的圆的外部，

则·>0，

又F(－2,0)，即·＝(x1＋2，y1)·(x2＋2，y2)

＝x1x2＋2(x1＋x2)＋y1y2＋4>0.

整理得m(m＋3)>0，

即m<－3或m>0.②

由①②可得m的取值范围是(－2，－3)∪(0,2)．

1． 求轨迹与轨迹方程的注意事项

(1)求轨迹方程的关键是在纷繁复杂的运动变化中，发现动点P的运动规律，即P点满足的等量关系，因此要学会动中求静，变中求不变．

(2)求出轨迹方程后，应注意检验其是否符合题意，既要检验是否增解(即以该方程的某些解为坐标的点不在轨迹上)，又要检验是否丢解(即轨迹上的某些点未能用所求的方程表示)．检验方法：研究运动中的特殊情形或极端情形．

2． 定点、定值问题的处理方法

定值包括几何量的定值或曲线过定点等问题，处理时可以直接推理求出定值，也可以先通过特定位置猜测结论后进行一般性证明．对于客观题，通过特殊值法探求定点、定值能达到事半功倍的效果．

3． 圆锥曲线的最值与范围问题的常见求法

(1)几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决；

(2)代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立起目标函数，再求这个函数的最值，在利用代数法解决最值与范围问题时常从以下五个方面考虑：

①利用判别式来构造不等关系，从而确定参数的取值范围；

②利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；

③利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；

④利用基本不等式求出参数的取值范围；

⑤利用函数的值域的求法，确定参数的取值范围.

设直线l：y＝k(x＋1)与椭圆x2＋3y2＝a2(a>0)相交于A、B两个不同的点，与x轴相交于点C，记O为坐标原点．

(1)证明：a2>；

(2)若＝2，求△OAB的面积取得最大值时的椭圆方程．

(1)证明　依题意，直线l显然不平行于坐标轴，

故y＝k(x＋1)可化为x＝y－1.

将x＝y－1代入x2＋3y2＝a2，消去x，

得y2－＋1－a2＝0， ①

由直线l与椭圆相交于两个不同的点，得

Δ＝－4(1－a2)>0，

整理得a2>3，

即a2>.

(2)解　设A(x1，y1)，B(x2，y2)由①，

得y1＋y2＝，

因为＝2，得y1＝－2y2，

代入上式，得y2＝.

于是，△OAB的面积S＝|OC|·|y1－y2|＝|y2|

＝≤＝.

其中，上式取等号的条件是3k2＝1，即k＝±.

由y2＝，可得y2＝±.

将k＝，y2＝－及k＝－，

y2＝这两组值分别代入①，

均可解出a2＝5.

所以，△OAB的面积取得最大值的椭圆方程是x2＋3y2＝5.

练习题

一、选择题

1． 已知方程＋＝1(k∈R)表示焦点在x轴上的椭圆，则k的取值范围是 (　　)

A．k<1或k>3 B．1<k<3 C．k>1 D．k<3

解：若椭圆焦点在x轴上，则，

解得1<k<3.选B.

2． △ABC的顶点A(－5,0)、B(5,0)，△ABC的内切圆圆心在直线x＝3上，则顶点C的轨迹方程是 (　　)

A.－＝1 B.－＝1

C.－＝1(x>3) D.－＝1(x>4)

解：如图|AD|＝|AE|＝8，|BF|＝|BE|＝2，

|CD|＝|CF|，

所以|CA|－|CB|＝8－2＝6.

根据双曲线定义，所求轨迹是以A、B为焦点，实轴长为6的双曲线的右支，方程为－＝1(x>3)．

3． 设M(x0，y0)为抛物线C：x2＝8y上一点，F为抛物线C的焦点，以F为圆心，|FM|为半径的圆和抛物线的准线相交，则y0的取值范围是 (　　)

A．(0,2) B．[0,2] C．(2，＋∞) D．[2，＋∞)

解：依题意得：F(0,2)，准线方程为y＝－2，

又∵以F为圆心，|FM|为半径的圆和抛物线的准线相交，且|FM|＝|y0＋2|，∴|FM|>4，即|y0＋2|>4，又y0≥0，∴y0>2.

4． 若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则·的最大值为 (　　)

A．2 B．3 C．6 D．8

解：设P(x0，y0)，则＋＝1，即y＝3－，

又因为F(－1,0)，

所以·＝x0·(x0＋1)＋y＝x＋x0＋3

＝(x0＋2)2＋2，

又x0∈[－2,2]，即·∈[2,6]，

所以(·)max＝6.

5． 已知中心在原点的椭圆与双曲线有公共焦点，左、右焦点分别为F1、F2，且两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形，若|PF1|＝10，椭圆与双曲线的离心率分别为e1，e2，则e1·e2的取值范围是 (　　)

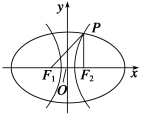
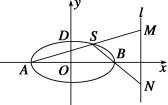
A．(0，＋∞) B．(，＋∞)

C．(，＋∞) D．(，＋∞)

解析　设椭圆与双曲线的半焦距为c，

PF1＝r1，PF2＝r2.

由题意知r1＝10，r2＝2c，且r1>r2,2r2>r1，

∴2c<10,2c＋2c>10，

∴<c<5⇒1<<4，

∴e2＝＝＝＝；

e1＝＝＝＝.

∴e1·e2＝＝>.

二、填空题

6． 直线y＝kx＋1与椭圆＋＝1恒有公共点，则m的取值范围是________．

解：∵方程＋＝1表示椭圆， ∴m>0且m≠5.

∵直线y＝kx＋1恒过(0,1)点，

∴要使直线与椭圆总有公共点，应有：＋≤1，m≥1，

∴m的取值范围是m≥1且m≠5.

7． 设F1、F2为椭圆＋y2＝1的左、右焦点，过椭圆中心任作一直线与椭圆交于P，Q两点，当四边形PF1QF2面积最大时，

1·2的值等于________．

解：易知当P，Q分别在椭圆短轴端点时，四边形PF1QF2面积最大．

此时，F1(－，0)，F2(，0)，不妨设P(0,1)，

∴1＝(－，－1)，2＝(，－1)，

∴1·2＝－2.

8． 已知抛物线方程为y2＝4x，直线l的方程为x－y＋4＝0，在抛物线上有一动点P到y轴的距离为d1，P到直线l的距离为d2，则d1＋d2的最小值为________．

解：过点P作抛物线的准线的垂线，垂足为A，交y轴于B，由抛物线方程为y2＝4x得焦点F的坐标为(1,0)，准线为x＝－1，则由抛物线的定义可得

d1＋d2＝|PA|－|AB|＋d2＝|PF|－1＋d2，

|PF|＋d2大于或等于焦点F点P到直线l，

即|PF|＋d2的最小值为＝，

所以d1＋d2的最小值为－1.

9． (2013·安徽)已知直线y＝a交抛物线y＝x2于A，B两点．若该抛物线上存在点C，使得∠ACB为直角，则a的取值范围为________．

解：以AB为直径的圆的方程为x2＋(y－a)2＝a，

由得y2＋(1－2a)y＋a2－a＝0.

即(y－a)[y－(a－1)]＝0，由已知解得a≥1.

三、解答题

10．已知直线x－2y＋2＝0经过椭圆C：＋＝1(a＞b＞0)的左顶点A和上顶点D，椭圆C的右顶点为B，点S是椭圆C上位于x轴上方的动点，直线AS，BS与直线l：x＝分别交于M，N两点．

(1)求椭圆C的方程；

(2)求线段MN的长度的最小值．

解　(1)如图，由题意得椭圆C的左顶点为A(－2,0)，上顶点为D(0,1)，即a＝2，b＝1.

故椭圆C的方程为＋y2＝1.

(2)直线AS的斜率显然存在且不为0，

设直线AS的方程为y＝k(x＋2)(k＞0)，解得M(，)，且将直线方程代入椭圆C的方程，

得(1＋4k2)x2＋16k2x＋16k2－4＝0.

设S(x1，y1)，由根与系数的关系得(－2)·x1＝.

由此得x1＝，y1＝，即S(，)．

又B(2,0)，则直线BS的方程为y＝－(x－2)，

联立直线BS与l的方程解得N(，－)．

∴|MN|＝＝＋≥2＝.

当且仅当＝，即k＝时等号成立，故当k＝时，线段MN的长度的最小值为.

11．在平面直角坐标系中，点P(x，y)为动点，已知点A(，0)，

B(－，0)，直线PA与PB的斜率之积为－.

(1)求动点P的轨迹E的方程；

(2)过点F(1,0)的直线l交曲线E于M，N两点，设点N关于x轴的对称点为Q(M、Q不重合)，求证：直线MQ过x轴上一定点．

(1)解　由题知：·＝－.

化简得＋y2＝1(y≠0)．

(2)证明　方法一　设M(x1，y1)，N(x2，y2)，Q(x2，－y2)，

l：x＝my＋1，代入＋y2＝1(y≠0)整理得

(m2＋2)y2＋2my－1＝0.

y1＋y2＝，y1y2＝，

MQ的方程为y－y1＝(x－x1)，

令y＝0，得x＝x1＋

＝my1＋1＋＝＋1＝2.

∴直线MQ过定点(2,0)．

方法二　设M(x1，y1)，N(x2，y2)，Q(x2，－y2)，

l：y＝k(x－1)，代入＋y2＝1(y≠0)整理得

(1＋2k2)x2－4k2x＋2k2－2＝0，

x1＋x2＝，x1x2＝，

MQ的方程为y－y1＝(x－x1)，

令y＝0，得x＝x1＋

＝x1＋＝＝2.

∴直线MQ过定点(2,0)．

12．(2013·课标全国Ⅰ)已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.

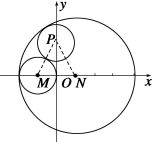
(1)求C的方程；

(2)l是与圆P，圆M都相切的一条直线，l与曲线C交于A、B两点，当圆P的半径最长时，求|AB|.

解　(1)设圆P的半径为r，则|PM|＝1＋r，|PN|＝3－r，

∴|PM|＋|PN|＝4>|MN|，

∴P的轨迹是以M、N为焦点的椭圆，左顶点除外，

且2a＝4,2c＝2，∴a＝2，c＝1，

∴b2＝a2－c2＝3.

∴P的轨迹曲线C的方程为＋＝1(x＝－2)．

(2)由(1)知：2r＝(|PM|－|PN|)＋2≤|MN|＋2＝4，

∴圆P的最大半径为r＝2.此时P的坐标为(2,0)．

圆P的方程为(x－2)2＋y2＝4.

①当l的方程为x＝0时，|AB|＝2，

②设l的方程为y＝kx＋b(k∈R)，

解之得：或.

∴l的方程为y＝x＋，y＝－x－.

联立方程化简：7x2＋8x－8＝0

∴x1＋x2＝－，x1x2＝－，

∴|AB|＝＝.